Parábola
Se denomina parábola al lugar
geométrico de los puntos de un plano que equidistan de una recta (eje o directriz) y un punto fijo llamado foco.
La parábola es la curva que
se obtiene como resultante de cortar un cono recto con
un plano paralelo a su generatriz sus
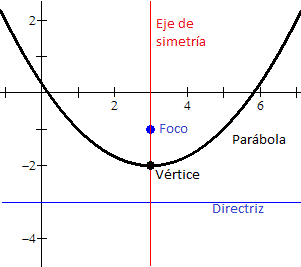
elementos fundamentales se muestran a en la imagen.
El punto F se denomina foco
y la recta d
es la directriz de la parábola.
La recta
que pasa por el foco y es perpendicular a
la directriz se llama eje de la
parábola.
En la figura de arriba el eje de la parábola coincide
con el eje Y. El punto en el que el eje corta a la parábola recibe el nombre de
vértice V y es el punto cuya distancia a la directriz es mínima.
La distancia entre el vértice y el foco se conoce como
Distancia focal o Radio focal.
Propiedades
• Es una curva abierta, consiste en dos arcos de curva (ramas)
sin puntos comunes que se prolongan ilimitadamente.
• Tiene dos ejes de simetría perpendiculares; por tanto, es
centralmente simétrica y tiene un centro.
• Un eje de simetría no contiene puntos de la curva
Ecuación
La ecuación de una parábola es
y - y0 = a (x - x0)2. Esta ecuación es la parábola con eje vertical y cuyo
vértice es (x0, y0).
Aplicaciones
La parábola encuentra su
aplicación en muchas ramas de las Ciencias aplicadas, debido a que las gráficas
de ecuaciones cuadráticas son parábolas. Por ejemplo, la trayectoria ideal del
movimiento de los cuerpos bajo la influencia de la gravedad.
Es empleada también en la
construcción de antenas satelitales aprovechando el principio de que un espejo
parabólico refleja de forma paralela los rayos emitidos desde su foco al igual
que los radiotelescopios que también se basan en la concentración de las
señales recibidas.
La concentración de la
radiación solar en un punto mediante un reflector parabólico es empleada en las
cocinas solares.